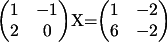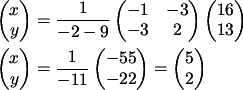OPERASI PERKALIAN BARIS ELEMENTER
Perkalian OBE Operasi Baris Elementer (OBE) merupakan suatu operasi yang diterapkan pada baris suatu matriks. OBE bisa digunakan untuk menentukan invers suatu matriks dan menyelesaikan suatu sistem persamaan linear (SPL).
Operasi Baris Elementer (OBE) adalah salah satu alternatif dalam menyelesaikan suatu bentuk matriks seperti menentukan invers matriks dan penerapan matriks pada sistem persamaan linear menggunakan dua cara yaitu "Eliminasi Gauss" dan "Eliminasi Gauss-Jordan".